Index > Course > 2021-04-15: Decision Trees and my own Experiment

2021-04-15: Decision Trees and my own Experiment

There are two things left in the class.

Assignment 6
- Consists of two case studies
  - Predict the values of Monroe county houses
  - Did the Prof save money with a wood burning stove?
- Goes pretty in-depth
Test 2
- Non-cumulative

Decision Trees

Not in assignment 6, but on the test

You have a choice between:

Receiving $100
3 to 1 odds of getting $70 or $200

digraph G {
    /* Entities */
    d1  [label="Decision 1", shape="square"]
    o1  [label="$100", shape="circle"]
    d2  [label="Random Choice", shape="rectangle"]
    o2  [label="$70", shape="circle"]
    o3  [label="$200", shape="circle"]
    /* Relationships */
    d1 -> o1 [label="100%"];
    d1 -> d2;
    d2 -> o2 [label="75%"];
    d2 -> o3 [label="25%"];
}

Outputs are worth some value. Solve the tree from right to left. (Bottom to Top in my graph). When you reach a chance node, calculate its expected value. When you reach a decision node, give it the value of the highest downstream chance node.

Me, Messing around

You have a choice between:

Receiving $100
3 to 1 odds of getting $70 or $200

Using arithmetic mean, the second choice is worth $102. Using the geometric mean, it’s worth $91.

What if we simulate this? It costs $100 to play, and we get some amount back.

function simulate(){
    let bank = 0;
    let iterations = 1000000;
    for(let i=0; i<iterations; i++){
        bank -= 100;
        bank += Math.ceil(Math.random()*4) === 4 ? 200 : 70;
    }
    // return avg gain per play
    return bank/iterations;
}

I ran this a few times. Results ranged from 2.4 to 2.5, implying the gamble is worth $102.5, and the arithmetic mean is correct.

Let’s change up the code…

function simulate(){
    let bank = 1000; // start with 1k
    let iterations = 1000000; // 1m rounds
    for(let i=0; i<iterations; i++){
        if(bank < 100){
            return (bank - 1000)/i;
        }
        bank -= 100;
        bank += Math.ceil(Math.random()*4) === 4 ? 200 : 70;
    }
    return (bank-1000)/iterations;
}

Most of the time, the game ends with an average return of $2.40 per turn. However, sometimes the player goes bankrupt before completing all million rounds. Let’s run the simulation 1000 times, and record the results:

function metaSim(){
    let wins = 0;
    for(let i=0; i<1000; i++){
        wins += simulate() > 0 ? 1 : 0;
    }
    console.log(`${wins} out of 1000 games survived. Win rate is ${Math.round(wins/10)}%`);
}

Each call to metaSim() simulates one billion rounds of the game. This takes about a minute. Running this multiple times took a while.

out of 1000 games survived. Win rate is 81%
out of 1000 games survived. Win rate is 77%
out of 1000 games survived. Win rate is 78%

Let’s say there is an 80% chance of 2.4% returns, and a 20% chance of -100% returns. Over many iterations, this means we expect -18% returns. You shouldn’t play this game. I wonder if I can simulate this, too.

I’ll simulate a shop that runs this game (starts with 1m) and sees multiple customers (each with 1k). Most customers will walk away with 2.5% returns - but the ones that go bankrupt can’t play the game anymore, so the shop will keep all of their money.

function shopSim(){
    // The shop starts with 1mil
    let shopBalance = 1000000;
    // 1k customers will start with 1k each
    for(let cNum=0; cNum<1000; cNum++){
        let customerBalance = 1000;
        for(let round=0; round<1000; round++){
            // Can the customer afford to play?
            if(customerBalance<100) break;
            // Can the store afford to play?
            if(shopBalance<200) break;
            // Play!
            let result = Math.random()*4 > 3 ? 200 : 70;
            customerBalance += result-100;
            shopBalance -= result-100;
        }
    }
    console.log(shopBalance);
}

If I’m right (you shouldn’t play this game) then the shop will end with more money than it started with.

Results:

No! The shop is going bankrupt! The customers are making a profit! What if I give the shop more money?

Starting the shop with 1 billion dollars:

All of these are less than 1 billion. The shop is losing money (roughly 3mil), but no longer going bankrupt (that’s hard to do when you start with 1b).

Here’s another idea - playing the game for more rounds, while it does let the customers make more money, also gives them more opportunities to go bankrupt. Let’s run the sim again, with 1mil rounds per customer instead of 1k:

(Once again, at 1b rounds, this takes a while):

100
150
180

The shop is going bankrupt again. It’s losing all billion dollars. This is a disaster!

I really need to dig-in and understand what’s going on. It’s time to break out the R code.

# How many rounds will the game last?
iterations <- 1000
# How much cash will players start with?
startingBalance <- 1000
# How many players will we simulate?
linesCount <- 30
# Function to simulate one player
doSim <- function(){
    results <- vector("numeric", iterations)
    balance <- startingBalance
    for(i in 1:iterations){
        random <- runif(1, min=0, max=4)
        if(random > 3){
            balance <- balance + 100
        }else{
            balance <- balance - 30
        }
        results[i] <- balance
    }
    results
}
# Run the function a bunch of times
lines <- list(linesCount)
for(l in 1:linesCount){
    lines[[l]] <- doSim()
}
# Find the range of the lines, for the graph
myRange <- range(lines[[1]])
for(l in 2:linesCount){
    myRange <- range(myRange, lines[[l]])
}
colors <- rainbow(linesCount) # colors are cool
# Plot the first line
plot(
    1:iterations,
    lines[[1]],
    ylim=myRange,
    type="l",
    col=colors[1],
    main="30 Simulated Games",
    ylab="Player Cash",
    xlab="Rounds Played"
)
# Plot the other lines
for(l in 2:linesCount){
    lines(1:iterations, lines[[l]], col=colors[l])
}
# Add some reference lines
abline(c(0,iterations),c(0,0))
abline(c(0,iterations),c(startingBalance,startingBalance*1.025))

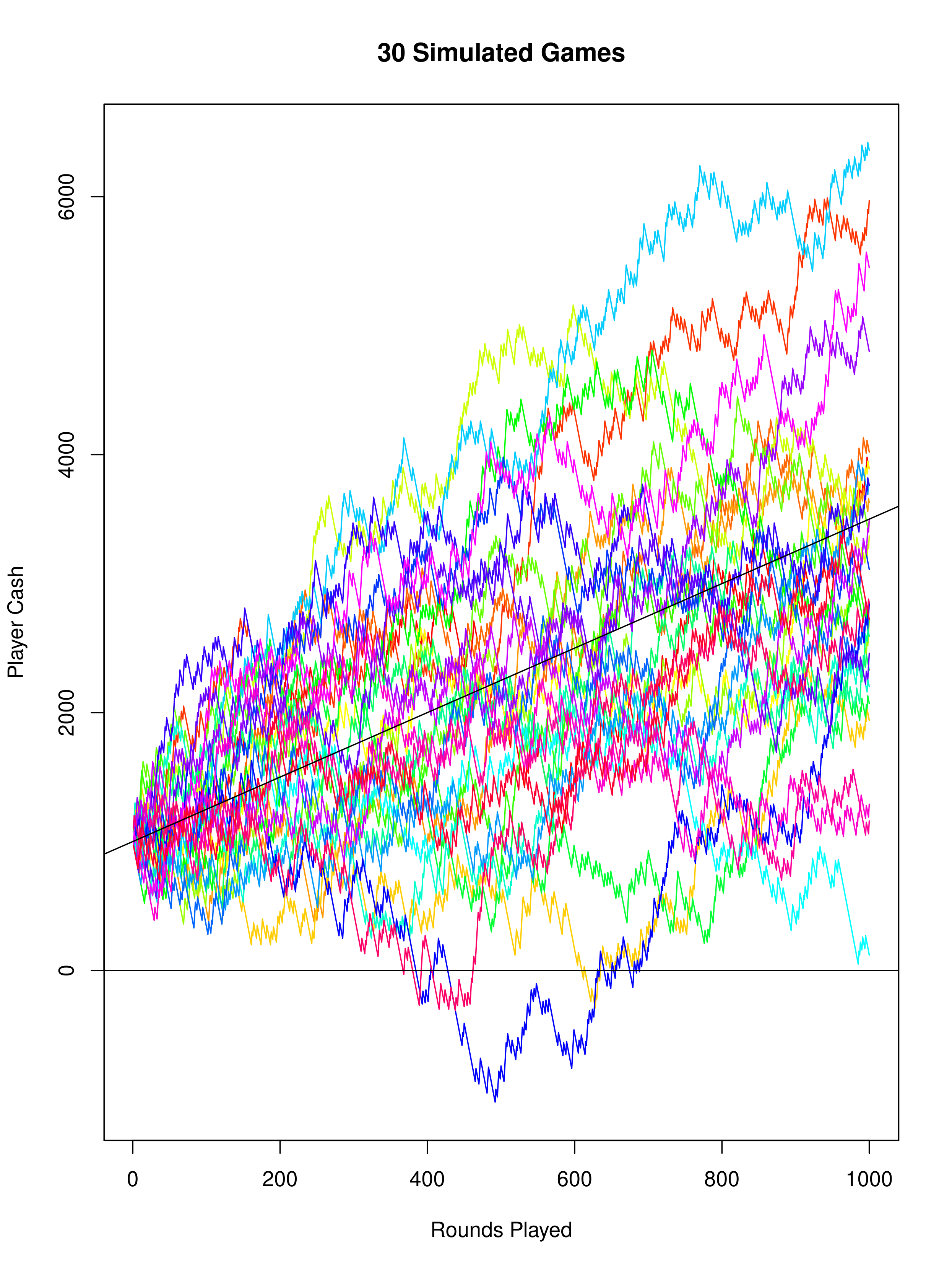
Now that’s some unicorn vomit. This graph teaches us some important lessons (Or at least makes more obvious things we should already know):

Everyone starts at the same point
From there, things very quickly spread out
Games that go up a lot, go up a lot
Games that go down, don’t actually go down that much
In general, players make money over time
The starting balance for a player is very relevant to weather or not they go bankrupt.

So what went wrong with the previous simulations? Those simulations let players play a lot of rounds, and we expect players to make roughly $2.50 per round. By the law of large numbers, this general increase gets more accurate with time.

So - if we’re the shop, we want to stop players from playing a lot of rounds. How can we do that?

If the players start with less money, they are more likely to go bankrupt
If the players get kicked out when they make too much, we can avoid “un-bounded” losses.

// TODO - JS that finds what percentage of players take any loss within the first 5 rounds.

Index > Course > 2021-04-15: Decision Trees and my own Experiment